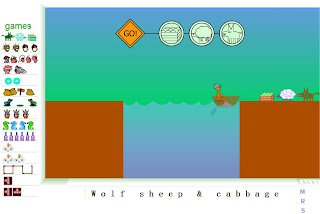
 JUEGO DE LOBO OVEJA Y REPOLLO
JUEGO DE LOBO OVEJA Y REPOLLO
PARA EMPEZAR EL JUEGO CLICK EN PLAY
EN ESTE JUEGO VERAS UN LOBO, UNA OVEJA Y UN REPOLLO LOS CUALES DEBERAS PASAR A LA OTRA ORILLA TENIENDO EN CUENTA QUE EL LOBO SE COME LA OVEJA Y QUE LA OVEJA SE COME EL REPOLLO.
DANDO CLICK EN LA IMAGEN QUE APARECE EN UN CIRCULO EN LA PARTE SUPERIOR SUBE EL ELEMENTO AL BOTE Y DANDO CLICK EN GO LO LLEVA A LA OTRA ORILLA, DANDO CLICK EN LA IMAGEN QUE APARECE EN UN CIRCULO EN LA PARTE SUPERIOR BAJA EL ELEMENTO SELECCIONADO.
1. SUBA LA OVEJA
2. LLEVELA A LA ORILLA
3. BAJE LA OVEJA Y VUELVA
4. SUBA EL LOBO Y VUELVA
5. BAJE EL LOBO SUBA LA OVEJA Y VUELVA
6. BAJE LA OVEJA SUBA EL REPOLLO Y VUELVA
7. BAJE EL REPOLLO Y VUELVA
8. SUBA LA OVEJA Y VUELVA
9. BAJE LA OVEJA FIN JUEGO
Bienvenido
View page in English
Contador de Visitas
Datos personales
Medidor internet
Portafolio de Servicios
lunes, 2 de marzo de 2009
jueves, 26 de febrero de 2009
JUEGO DE CANIBALES Y MISIONEROS
PARA EMPEZAR EL JUEGO CLICK EN PLAY
EN ESTE JUEGO VERAS 3 CANIBALES Y TRES MISIONEROS LOS CUALES DEBERAS PASAR A LA ORILLA IZQUIERDA QUEDANDO VACIA LA ORILLA DERECHA AL FINALIZAR EL JUEGO. DEBES TENER EN CUENTA QUE SI QUEDA MAYOR NUMERO DE CANIBALES QUE MISIONEROS EN ALGUNA DE LAS ORILLAS ESTOS SE COMEN A LOS MISIONEROS. DANDO CLICK EN MISIONERO O CANIBAL SUBE O BAJA DEL BOTE, DANDO CLICK EN EL ICONO GO SE DESPLAZA EL BOTE HACIA LA ORILLA. EL BOTE SIEMPRE DEBE IR OCUPADO PARA PODERSE DESPLAZAR AL MENOS POR UN TRIPULANTE.
MISIONEROS Y CANIBALES
1 MONTE UN CANIBAL Y UN MISIONERO EN EL BOTE
2 LLEVELO A LA ORILLA
3 BAJE EL CANIBAL Y VUELVA
4 BAJE EL MISIONERO Y SUBA DOS CANIBALES Y VUELVA
5 BAJE UN CANIBAL Y VUELVA
6 BAJE EL CANIBAL SUBA DOS MISIONEROS Y VUELVA
7 BAJE UN MISIONERO SUBA UN CANIBAL Y VUELVA
8 BAJE EL CANIBAL SUBA UN MISIONERO Y VUELVA
9 BAJE DOS MISIONEROS SUBA UN CANIBAL Y VUELVA
miércoles, 18 de febrero de 2009
Consultas: aquí definiremos las preguntas que formularemos a la base de datos con el fin de extraer y presentar la información resultante de diferentes formas (pantalla, impresora...)
Informe: permite preparar los registros de la base de datos de forma personalizada para imprimirlos.
Módulo: programa o conjunto de instrucciones en lenguaje Visual Basic: unidad básica de una base de datos. Un campo puede ser, por ejemplo, el nombre de una persona. Los nombres de los campos, no pueden empezar con espacios en blanco y caracteres especiales. No pueden llevar puntos, ni signos de exclamación o corchetes. Si pueden tener espacios en blanco en el medio. La descripción de un campo, permite aclarar información referida a los nombres del campo. El tipo de campo, permite especificar el tipo de información que cargaramos en dicho campo, esta puede ser:
Texto: para introducir cadenas de caracteres hasta un máximo de 255
Memo: para introducir un texto extenso. Hasta 65.535 caracteres
Numérico: para introducir números
Fecha/Hora: para introducir datos en formato fecha u hora
Moneda: para introducir datos en formato número y con el signo monetario
Autonumérico: en este tipo de campo, Access numera automáticamente el contenido
Sí/No: campo lógico. Este tipo de campo es sólo si queremos un contenido del tipo Sí/No, Verdadero/Falso, etc.
Objeto OLE: para introducir una foto, gráfico, hoja de cálculo, sonido, etc.
Hipervínculo: podemos definir un enlace a una página Web
Asistente para búsquedas: crea un campo que permite elegir un valor de otra tabla o de una lista de valores mediante un cuadro de lista o un cuadro combinado.
Registro: es el conjunto de información referida a una misma persona u objeto. Un registro vendría a ser algo así como una ficha.
domingo, 8 de febrero de 2009
 Esta funcion permite unir varios elementos de texto en uno solo
Esta funcion permite unir varios elementos de texto en uno solo
También se puede concatenar dos cadenas de caracteres o un carácter con una cadena para formar una cadena de mayor tamaño. Algunos ejemplos serían:
'a' concatenado 'b' --> "ab"
"ABCD" concatenado 'b' --> "ABCDb"
'a' concatenado "XYZ" --> "aXYZ"
"ABCD" concatenado "XYZ" --> "ABCDXYZ"
(texto1;texto2; ...)
Texto1, texto2... son de 2 a 255 elementos de texto que se unirán en un elemento de texto único. Los elementos de texto pueden ser cadenas de texto, números o referencias a celdas únicas.
Observaciones
También puede utilizar el operador de cálculo símbolo de "y" comercial (&) en lugar de la función CONCATENAR para unir elementos de texto. Por ejemplo =A1&B1 devuelve el mismo valor que =CONCATENAR(A1;B1).
Ejemplo
El ejemplo será más fácil de entender si lo copia a una hoja de cálculo en blanco.
Cómo copiar un ejemplo
Cree un libro o una hoja de cálculo en blanco.
Seleccione el ejemplo en el tema de Ayuda.
Nota No seleccione los encabezados de fila ni de columna.
Seleccionar un ejemplo de la Ayuda
Presione CTRL+C.
En la hoja de cálculo, seleccione la celda A1 y presione CTRL+V.
Para cambiar entre ver los resultados y ver las fórmulas que devuelven los resultados, presione CTRL+` (acento grave), o en la ficha Fórmulas, en el grupo Auditoría de fórmulas, haga clic en el botón Mostrar fórmulas.
1
2
3
4
A
Datos
Nombre apellido Nombre completo completo
martes, 3 de febrero de 2009
Dentro de un disco duro hay uno o varios platos (entre 2 y 4 normalmente, aunque hay hasta de 6 ó 7 platos), que son discos (de aluminio o cristal) concéntricos y que giran todos a la vez. El cabezal (dispositivo de lectura y escritura) es un conjunto de brazos alineados verticalmente que se mueven hacia dentro o fuera según convenga, todos a la vez. En la punta de dichos brazos están las cabezas de lectura/escritura, que gracias al movimiento del cabezal pueden leer tanto zonas interiores como exteriores del disco.
Cada plato tiene dos caras, y es necesaria una cabeza de lectura/escritura para cada cara (no es una cabeza por plato, sino una por cara). Si se mira el esquema Cilindro-Cabeza-Sector (más abajo), a primera vista se ven 4 brazos, uno para cada plato. En realidad, cada uno de los brazos es doble, y contiene 2 cabezas: una para leer la cara superior del plato, y otra para leer la cara inferior. Por tanto, hay 8 cabezas para leer 4 platos. Las cabezas de lectura/escritura nunca tocan el disco, sino que pasan muy cerca (hasta a 3 nanómetros) ó 3 millonésimas de milímetro. Si alguna llega a tocarlo, causaría muchos daños en el disco, rayándolo gravemente, debido a lo rápido que giran los platos (uno de 7.500 revoluciones por minuto se mueve a 120 km/h en el borde).

La importancia de un algoritmo radica en mostrar la manera de llevar a cabo procesos y resolver mecánicamente problemas matemáticos o de otro tipo. Al igual que las funciones matemáticas, los algoritmos reciben una entrada y la transforman en una salida, comportándose como una caja negra. Sin embargo, no toda caja negra que convierta una entrada en una salida se puede considerar un algoritmo: para que un algoritmo pueda ser considerado como tal, debe ser una secuencia ordenada, finita y definida (formalización de su comportamiento) de instrucciones. De este modo se puede seguir y predecir el comportamiento del algoritmo para cualquier entrada posible (salvo algoritmos probabilistas, que tiene usualmente una salida distinta), a partir del seguimiento de esa secuencia de instrucciones, que como es ordenada y definida, no da lugar a ambigüedades y puede seguirse su traza.
El concepto de algoritmo, aunque similar y obviamente relacionado, no debe confundirse con el concepto de programa. Mientras el primero es la especificación de un conjunto de pasos (operaciones, instrucciones, órdenes,...) orientados a la resolución de un problema (método), el segundo es ese conjunto de operaciones especificadas en un determinado lenguaje de programación y para un computador concreto, susceptible de ser ejecutado (o compilado o interpretado). Un algoritmo, estrictamente hablando, no puede ejecutarse hasta que se implementa, ya sea en un lenguaje de programación, en un circuito eléctrico, en un aparato mecánico, usando papel y lápiz, o en algún otro modelo de computación.
La mayoría de los algoritmos involucran métodos de organizar los datos que intervienen en el cómputo. Estos objetos creados son llamados, de esta manera la estructura de los datos, y también son objetos centrales del estudio en la informática. De esta forma, los algoritmos y estructuras de los datos van siempre de la mano. Los algoritmos simples pueden dar lugar a una estructura de datos complicada y, recíprocamente, los algoritmos complicados pueden usar estructuras de los datos simples.
Cuando usamos una computadora para ayudarnos a resolver un problema, nos enfrentamos típicamente con varios posibles esquemas. Para los problemas pequeños, lo que apenas importa es que lo usemos, con tal de que se tenga uno que resuelva el problema correctamente. Para los problemas grandes (o aplicaciones dónde nosotros necesitamos resolver un gran número de problemas pequeños), sin embargo, nos motivamos en inventar métodos que usan tiempo eficazmente de forma rápida como sea posible.
Cuando un programa de computadora es grande o complejo, este será desarrollado con mucho esfuerzo, ya que se debe comprender y definir el problema a ser resuelto, manejando su complejidad, y descomponiéndolo en partes más pequeñas que puedan resolverse más fácilmente. A menudo, muchos de los algoritmos que se necesitan, después de la descomposición son triviales al instrumento.
Teoría de la computabilidad
Formalmente, un algoritmo calcula a una función. Como cualquier conjunto finito es numerable, y cualquier conjunto numerable se puede expresar en términos del conjunto de los números naturales (infinito, pero numerable, de hecho no existe otro conjunto más grande que sea también numerable), en esencia, todo algoritmo calcula a funciones definidas en los números naturales. En este punto, una función está parcial o totalmente definida. Una función es parcial cuando hay números naturales que no pertenecen a su dominio (es decir, hay números naturales sobre los que no está definida la función), y una función es total en caso contrario.
Si una función es parcial, el algoritmo que lo calcula solo devolverá un resultado (es decir gasta un tiempo de cálculo finito) para los valores en los que la función está definida, no devolviendo resultado (el tiempo de cálculo es infinito) para el resto de valores. Si un algoritmo que calcula a una función parcial devolviera un resultado para los valores no definidos de la función, entonces no calcularía a esa función sino a otra. Del mismo modo, un algoritmo que calcula a una función total siempre devuelve un resultado para todo valor, y que al igual que las funciones parciales, éste debe coincidir exactamente con el valor que devuelve la función a la que calcula; y reiterativamente, en caso contrario, no calcularía a esa función sino a otra. Así, todo algoritmo calcula a una función definida sobre los números naturales, sea cuál sea ésta su naturaleza.
Toda función para la cual exista un algoritmo que lo calcule se denomina función computable (parcialmente computable o totalmente computable depende del grado de definición de la función en cuestión), pero existen funciones que no pueden ser calculadas como la función de Ackermann, a este último tipo de funciones se las denomina funciones no computables.



















